This item is taken from Cambridge International AS and A Level Mathematics (9709) Statistics 1 Paper 6 of October/November 2007.
--------------------------------------------------------------------------------------------------------------------------
To deal with this item, let us summarize the details of the problem:
(a) Syllabus area: Discrete Random Variables
(b) Formula/Concept needed:
> discrete random variables
> probability of distribution of discrete random variables
> expectation (mean) and variance of discrete random variables
--------------------------------------------------------------------------------------------------------------------------
To deal with this item, let us summarize the details of the problem:
(a) Syllabus area: Discrete Random Variables
(b) Formula/Concept needed:
> discrete random variables
> probability of distribution of discrete random variables
> expectation (mean) and variance of discrete random variables
Before we answer the items, let us encircle the important clues/phrases.
It means that
The following table shows the probability distribution of the discrete random variable in terms of p.
To solve for p, we equate the sum of the probabilities to one (1).
Hence, the value of p is 1/6.
For part (ii),
It means
Let us complete first the probability distribution of the discrete random variable using the value of p from (i). You may use the unsimplified or simplified fraction form of the probabilities. The calculation is shown below the table.
To find the expectation or mean, we need to multiply the values (x) of the random variable with their corresponding probabilities (p). That is
Using the probabilities on the tables,
or
To find the variance, use the following
Using the values of p from the table,
----------------------------------------------------------------------------------------------------------------------------------------------------
Your comments and suggestions are welcome here. Write them in the comment box below.
Thank you and God bless!
It means that
The following table shows the probability distribution of the discrete random variable in terms of p.
To solve for p, we equate the sum of the probabilities to one (1).
Hence, the value of p is 1/6.
For part (ii),
It means
Let us complete first the probability distribution of the discrete random variable using the value of p from (i). You may use the unsimplified or simplified fraction form of the probabilities. The calculation is shown below the table.
To find the expectation or mean, we need to multiply the values (x) of the random variable with their corresponding probabilities (p). That is
Using the probabilities on the tables,
or
To find the variance, use the following
Using the values of p from the table,
OR
Hence, the mean of the discrete random variable is 4/3 and the variance is 68/9.----------------------------------------------------------------------------------------------------------------------------------------------------
Your comments and suggestions are welcome here. Write them in the comment box below.
Thank you and God bless!











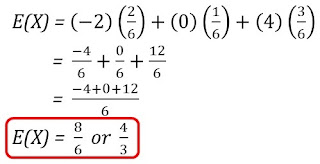





















No comments:
Post a Comment
Write your comments and suggestions here.