Latest Posts

Home Binomial Expansion

Binomial Expansion

AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals


AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals

 This item is taken from Cambridge International AS and A Level Mathematics (9709) Pure Mathematics 1 Paper 11 of May/June 2010.

--------------------------------------------------------------------------------------------------------------------------
To deal with this item, let us summarize the details of the problem:
   (a) Syllabus area: Series  
   (b) Formula/Concept needed: 
            > Binomial Expansion
            > rth term or specific term of a binomial expansion
            > Product of two binomials

 Recall the Binomial Expansion Theorem and the rth term of the Binomial Expansion.
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals

For part (i),
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
It means that
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
To do that, we need to identify the given values:
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
Substituting the values of a, b, n and r,
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
Simplify each of the terms
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals

 Hence, the first three terms of the expansion is 
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals


 For part (ii),
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
It means that
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
Take note that we are finding the
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
Since we are only interested in finding the coefficient of x, then
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
From part (i), we already have the term with x and x^3.
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals
Simplifying and combining like terms,
AS Level,A level,Exam,CIE,Cambridge,past papers,solutions,advance level,binomial expansion,product,powers,ascending power, descending power,first terms,binomial,series,sequences,Pascals

Hence, the coefficient of x in the product of the two binomials is 240. 

 ----------------------------------------------------------------------------------------------------------------------------------------------------
Your comments and suggestions are welcome here. Write them in the comment box below.

Thank you and God bless!   


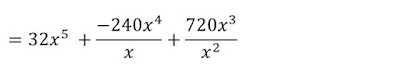
No comments:

Post a Comment

Write your comments and suggestions here.

Subscribe to: Post Comments (Atom)

CIE Math Solutions Designed by Templateism.com Copyright © 2014

Theme images by 5ugarless. Powered by Blogger.