Latest Posts

Home Product of Matrices

Product of Matrices

IGCSE,Mathematics,0580,Product of Matrices,Order of matrix,multiply matrix,matrix times matrix,square of a matrix,CIE,revisions
This item is taken from IGCSE Mathematics (0580) Paper 42 of May/June 2013.


To deal with this item, let us summarize the details of the problem:
   (a) Syllabus area: Matrices
   (b) Specific topic: Operations on Matrices

The common mistake students do with this item is to get directly the square of each element of the matrix. Here is the common wrong solution and answer:
IGCSE,Mathematics,0580,Product of Matrices,Order of matrix,multiply matrix,matrix times matrix,square of a matrix,CIE,revisions
Take note that:
IGCSE,Mathematics,0580,Product of Matrices,Order of matrix,multiply matrix,matrix times matrix,square of a matrix,CIE,revisions
It means that it is the product of matrix D multiplied to itself.
IGCSE,Mathematics,0580,Product of Matrices,Order of matrix,multiply matrix,matrix times matrix,square of a matrix,CIE,revisions
Before you start multiplying, determine first the order (dimension) of each matrix and the order of the resulting matrix.
IGCSE,Mathematics,0580,Product of Matrices,Order of matrix,multiply matrix,matrix times matrix,square of a matrix,CIE,revisions
It is possible to multiply the matrices since the number of columns of the first is equal to the number of rows of the second matrix. Follow the method of multiplying matrices - multiply each row of the first to each column of the second. That is
IGCSE,Mathematics,0580,Product of Matrices,Order of matrix,multiply matrix,matrix times matrix,square of a matrix,CIE,revisions
Simplify.
IGCSE,Mathematics,0580,Product of Matrices,Order of matrix,multiply matrix,matrix times matrix,square of a matrix,CIE,revisions
Therefore, 
IGCSE,Mathematics,0580,Product of Matrices,Order of matrix,multiply matrix,matrix times matrix,square of a matrix,CIE,revisions
----------------------------------------------------------------------------------------------------------------------------------
Your comments and suggestions are welcome here. Write them in the comment box below.

Thank you and God bless!

www.mathematicsrealm.blogspot.com
www.learnatmathematicsrealm.blogspot.com
www.igcseatmathematicsrealm.blogspot.com

www.ciemathsolutions.blogspot.com

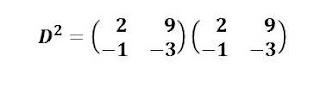
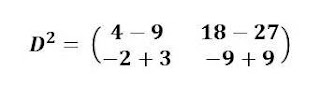
No comments:

Post a Comment

Write your comments and suggestions here.

Subscribe to: Post Comments (Atom)

CIE Math Solutions Designed by Templateism.com Copyright © 2014

Theme images by 5ugarless. Powered by Blogger.