This item is taken from IGCSE Mathematics (0580) Paper 22 of October/November 2013.
To deal with this item, let us summarize the details of the problem:
(a) Syllabus area: Vectors
(b) Specific topic: Vectors, Position Vectors, Addition/Subtraction of Vectors
(c) Concept Needed:
To deal with this item, let us summarize the details of the problem:
(a) Syllabus area: Vectors
(b) Specific topic: Vectors, Position Vectors, Addition/Subtraction of Vectors
(c) Concept Needed:
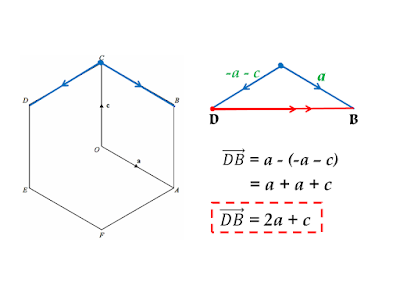
We cannot get the direct value of BE using the given vectors. Instead, we can find the value of OB first, then use the relation of the vectors BE = 2BO.
Considering vectors OC and CB, the resultant is vector OB. This uses the concept of triangle law of vector addition, since vector OC and CB are in a nose to tail position.
However, we are finding BO. Hence, we can reverse the directions and find the resultant BO in terms of a and c.
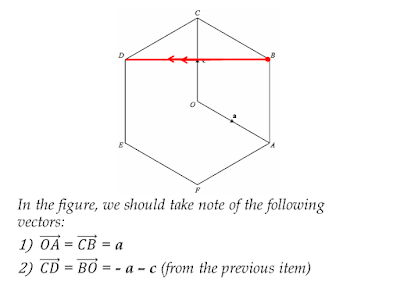
For (b), let us start with the relations of the vectors needed.
For (iii), we should take note that it is a position vector. It means that the vector starts with O then ends with E. Hence, we are finding vector OE.
Using the relation of vector OE and vector BE,
Therefore,
Using the relation of vector OE and vector BE,
Therefore,
---------------------------------------------------------------------------------------------------------------
Your comments and suggestions are welcome here. Write them in the comment box below.
Thank you and God bless!
Thank you and God bless!





























No comments:
Post a Comment
Write your comments and suggestions here.